Algorithm complexity
Reading time15 minIn brief
Article summary
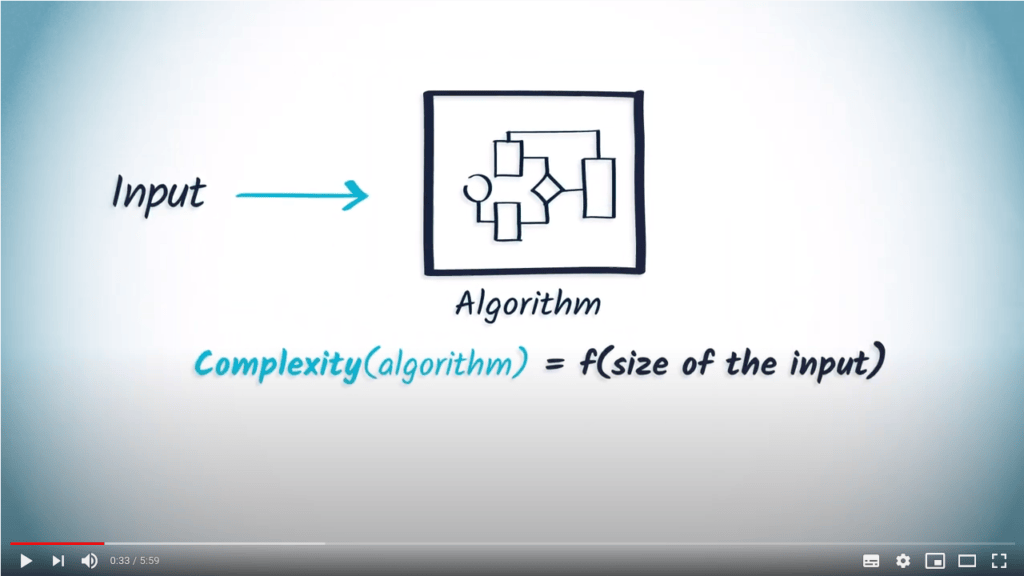
In this article, you will learn an important theoretical notion to compare algorithms: complexity. In the previous articles you already have met some notations like $O(n)$. We will now make it more explicit.
Main takeaways
-
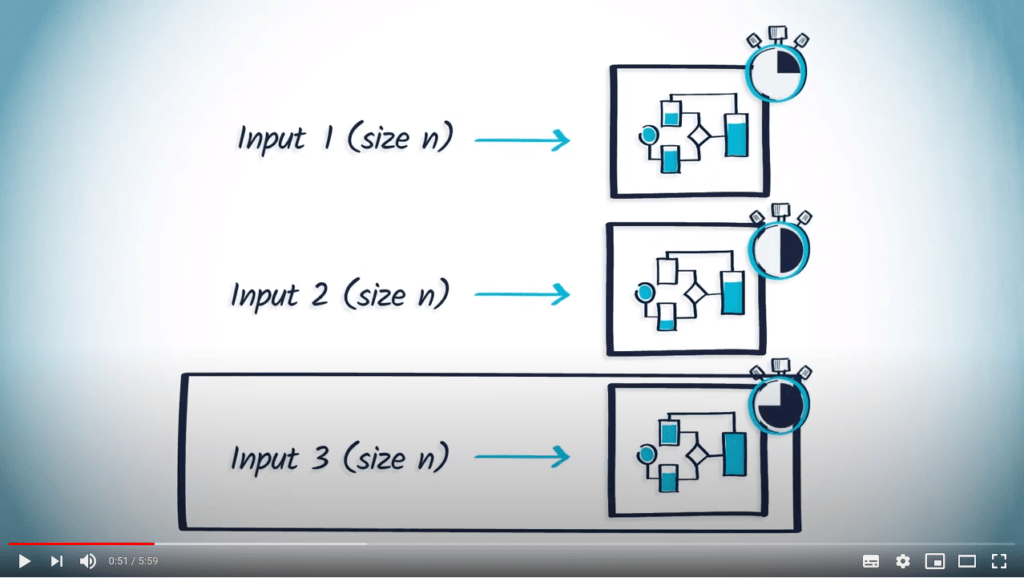
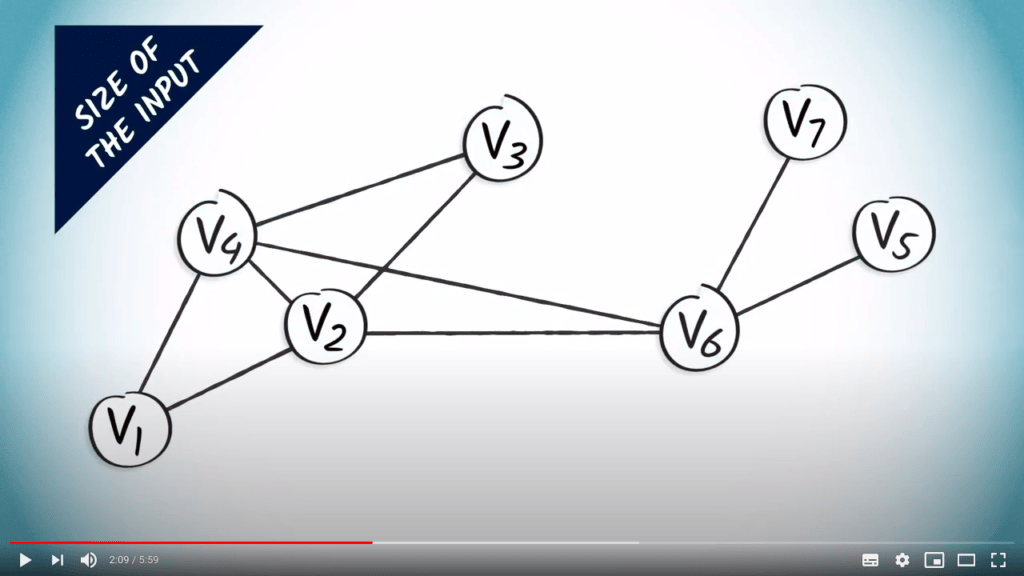
Complexity of an algorithm is an abstract measure of its needed time to complete, as a function of its inputs.
-
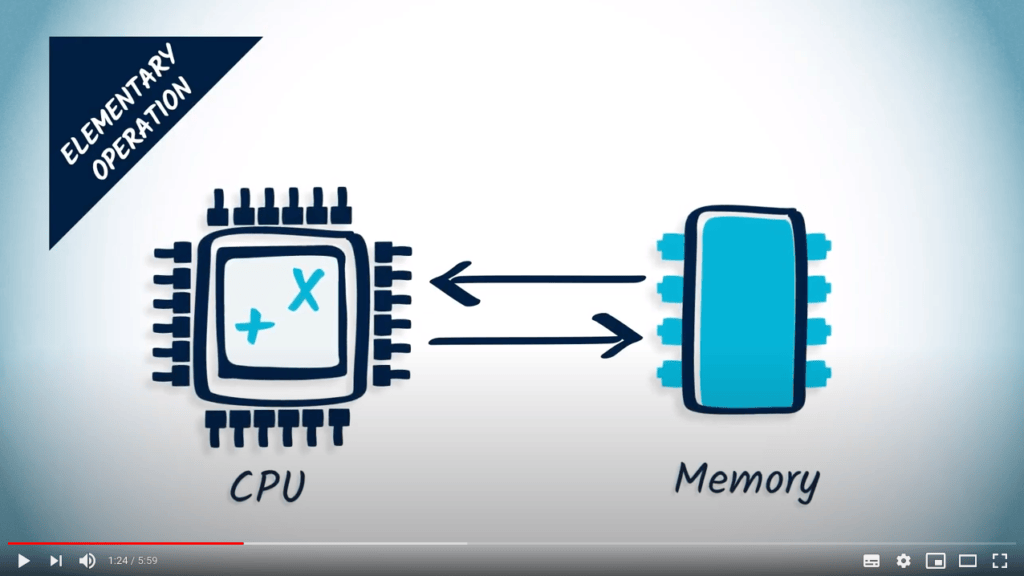
It makes abstraction of machine-specific elements such as CPU performance, contrary to time measurements.
-
Complexity is generally given in worst-case scenario.
-
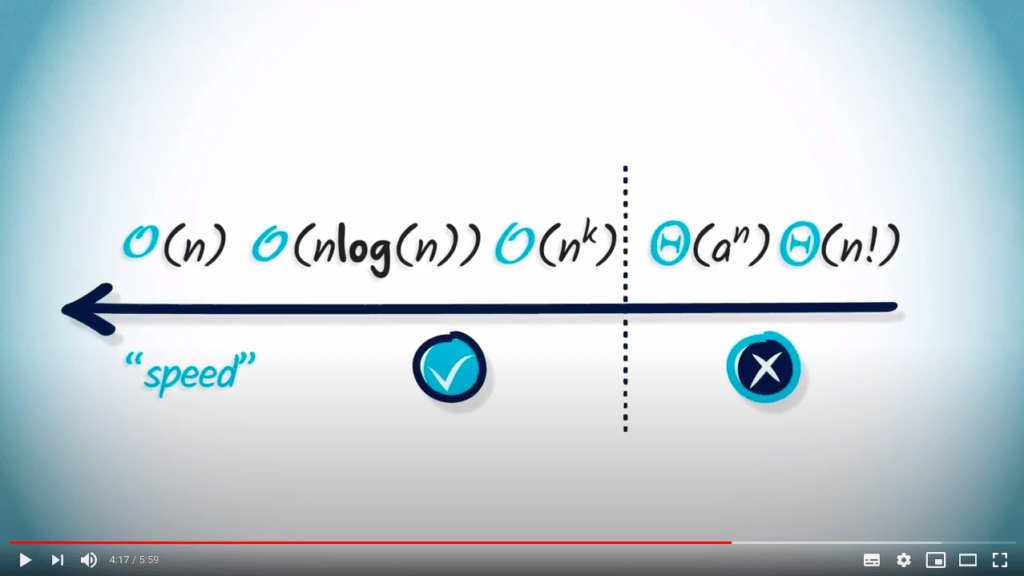
We use the notation $O(\cdot)$, as we are interested in the order of the time needed, asymptotically.
Article contents
1 — Video
Please check the video below. You can also read the transcripts if you prefer.
To go further
The content of this section is optional. It contains additional material for you to consolidate your understanding of the current topic.
2 — Remarks on complexity of algorithms
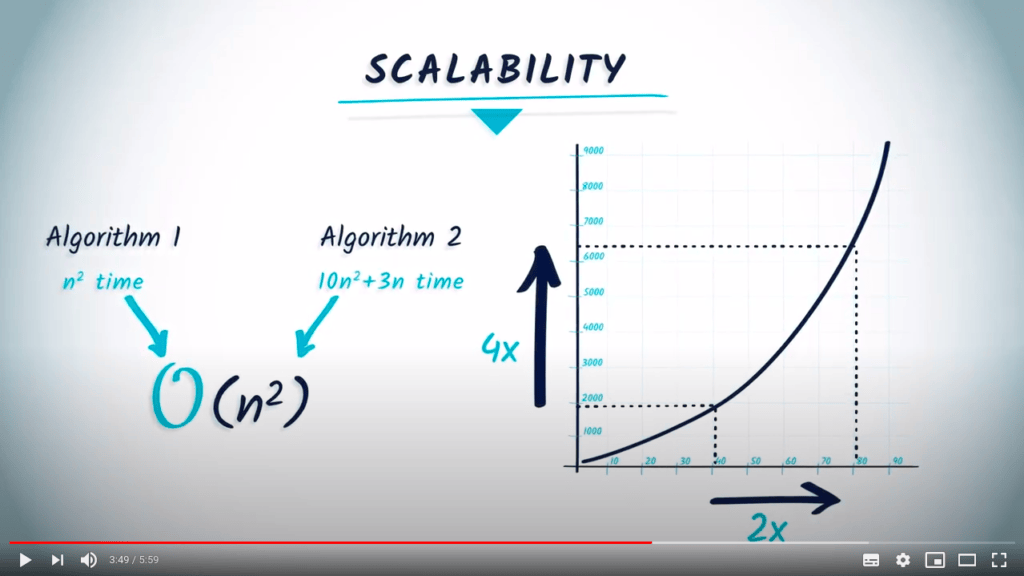
It is often tempting to compare the asymptotic behaviors of the complexities of algorithms to draw conclusions. That’s why they are most often used, but sometimes the devil is in the details.
2.1 — Worst case
The complexity of an algorithm is defined as the number of elementary operations required for the worst possible case. In practice, the algorithm can be fast in almost all cases. An example of a famous algorithm with this property is the simplex algorithm.
2.2 — Asymptotic behavior
Let us take two functions $f$ and $g$ of $n$. We can quite easily have $f(n) = O(g(n))$ and yet $f(n) > g(n)$ for all $n > N$. In practice, some algorithms may have a more favorable asymptotic behavior but are much slower in practice. A famous example is the primality test.
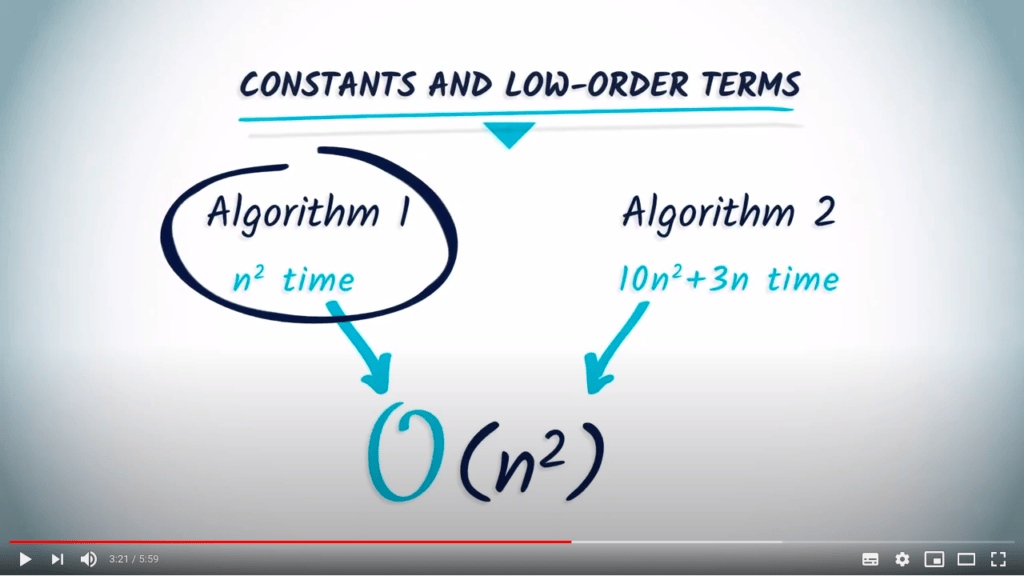
2.3 — The importance of constants
Writings of asymptotic behavior ignores constants. In particular, we can write $10^{10^{10^{10^{10}}}} n^2 = O(n^2)$. However, an algorithm whose complexity is exactly $10^{10^{10^{10^{10}}}} n^2 is 10^{10^{10^{10^{10}}}}$ times slower than an algorithm whose complexity is exactly $n^2$.
To go beyond
The content of this section is very optional. We suggest you directions to explore if you wish to go deeper in the current topic.
This function that grows very rapidly sometimes appears in the complexity of some highly demanding algorithms.
A popular algorithm for solving problems, with a complexity of $O(2^n)$
Determining if a number is prime has a favorable asymptotic behavior but is slow in practice.